Precision
Date: 1740
- 1 : the quality or state of being precise : exactness
- 2 a : the degree of refinement with which an operation is performed or a measurement stated — compare accuracy
- b : the accuracy (as in binary or decimal places) with which a number can be represented usually expressed in terms of the number of computer words available for representation <double precision arithmetic permits the representation of an expression by two computer words>
Description
The accuracy of a measurement system is the degree of closeness of measurements of a quantity to its actual (true) value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which repeated measurements under unchanged conditions show the same results. Although the two words can be synonymous in colloquial use, they are deliberately contrasted in the context of the scientific method. Accuracy indicates proximity of measurement results to the true value, precision to the repeatability or reproducibility of the measurement.
A measurement system can be accurate but not precise, precise but not accurate, neither, or both. For example, if an experiment contains a systematic error, then increasing the sample size generally increases precision but does not improve accuracy. Eliminating the systematic error improves accuracy but does not change precision.
A measurement system is called valid if it is both accurate and precise. Related terms are bias (non-random or directed effects caused by a factor or factors unrelated by the independent variable) and error (random variability), respectively.
The terminology is also applied to indirect measurements, that is, values obtained by a computational procedure from observed data.
In addition to accuracy and precision, measurements may have also a measurement resolution, which is the smallest change in the underlying physical quantity that produces a response in the measurement. Its precision, however, may be low.
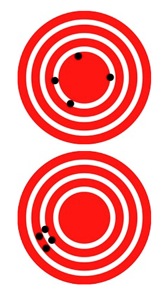
Target Analogy
Accuracy is the degree of veracity while precision is the degree of reproducibility. The analogy used here to explain the difference between accuracy and precision is the target comparison. In this analogy, repeated measurements are compared to arrows that are shot at a target. Accuracy describes the closeness of arrows to the bullseye at the target center. Arrows that strike closer to the bullseye are considered more accurate. The closer a system's measurements to the accepted value, the more accurate the system is considered to be.
To continue the analogy, if a large number of arrows are shot, precision would be the size of the arrow cluster. (When only one arrow is shot, precision is the size of the cluster one would expect if this were repeated many times under the same conditions.) When all arrows are grouped tightly together, the cluster is considered precise since they all struck close to the same spot, even if not necessarily near the bullseye. The measurements are precise, though not necessarily accurate.
However, it is not possible to reliably achieve accuracy in individual measurements without precision—if the arrows are not grouped close to one another, they cannot all be close to the bullseye. (Their average position might be an accurate estimation of the bullseye, but the individual arrows are inaccurate.) See also circular error probable for application of precision to the science of ballistics.[1]